Salzer's Method for Numerical Evaluation of Inverse Laplace Transform Involving a Bessel Function
Salzer's Method for Numerical Evaluation of Inverse Laplace Transform Involving a Bessel Function
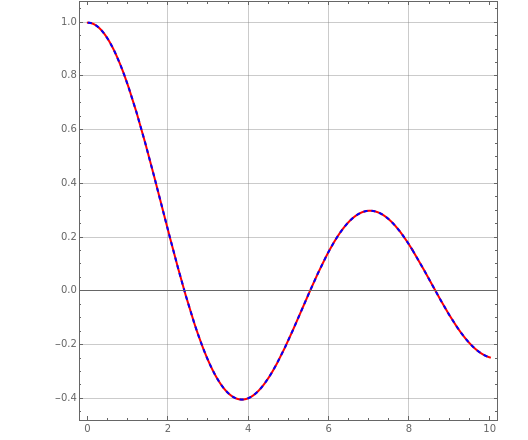
This Demonstration shows the numerical inversion of Laplace transforms using Herbert E. Salzer's method [1]. The test function is , where the user sets the parameter . The exact inverse Laplace transform is given by , where is the Bessel function of the first kind of order zero. The error (i.e. the difference between the exact inverse and the numerical inverse) is also given. The numerical method fails at large (see the first snapshot) and can only serve as a quick-and-dirty technique for the inversion of Laplace transforms.
F(s)=ℒ(f(t))=+
1
2
a
2
s
a
f(t)=(at)
J
0
J
0
t