Recurrence Network Measures for the Logistic Map
Recurrence Network Measures for the Logistic Map
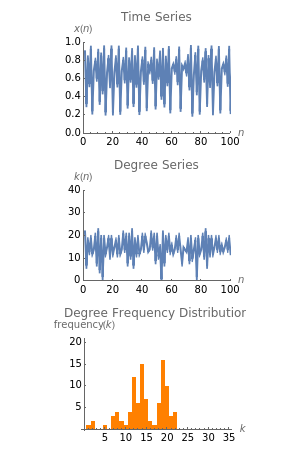
The degree centrality and clustering coefficient of nodes in the recurrence network of a time series reveal complementary geometrical properties of the dynamics in phase space. This helps to distinguish between the various dynamical regimes of a complex nonlinear system.
The logistic map provides a good model for dynamical transitions among regular, laminar, and chaotic behavior of a dynamical system. The evolution and properties of the time series depend on the control parameter .
a
Observe how the degree and clustering series and frequency distribution evolve as you change the control parameter . Can you identify periodic windows in a sea of chaos? As you increase the recurrence threshold , the recurrence network measures slowly approach those expected for a fully connected network.
a
ϵ