Rectangular Pulse and Its Fourier Transform
Rectangular Pulse and Its Fourier Transform
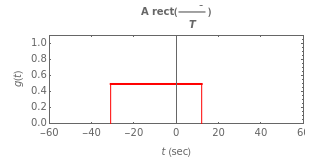
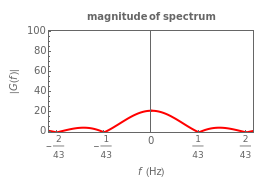
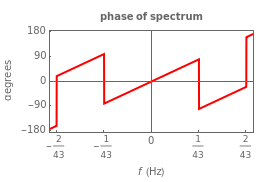
This Demonstration illustrates the relationship between a rectangular pulse signal and its Fourier transform. There are three parameters that define a rectangular pulse: its height , width in seconds, and center . Mathematically, a rectangular pulse delayed by seconds is defined as and its Fourier transform or spectrum is defined as .
A
T
t
0
t
0
g(t-)=Arect=
t
0
t-
t
0
T
A | t- t 0 T 1 2 |
0 | otherwise |
G(f)=ATsinc(πfT)exp(-i2πf)
t
0
This Demonstration illustrates how changing affects its spectrum. Both the magnitude and phase of the spectrum are displayed.
g(t)