Reaction-Diffusion in a Two-Dimensional Catalyst Pellet

collocation points

21

γ

25

2

ϕ

0.8

b

6

Consider the reaction-diffusion in a two-dimensional catalyst pellet with governing equations and boundary condition:

Le

u

t

=

u

xx

+

u

yy

+b

2

ϕ

(1-v)

γu/(γ+u)

e

,

v

t

=

v

xx

+

v

yy

+

2

ϕ

(1-v)

γu/(γ+u)

e

,

u=v=0

at

x=y=±1

and

t=0

,

where

2

ϕ

is the Thiele modulus,

b

is the adiabatic temperature rise (the Prater temperature),

γ

is the activation energy, and

Le

is the Lewis number.

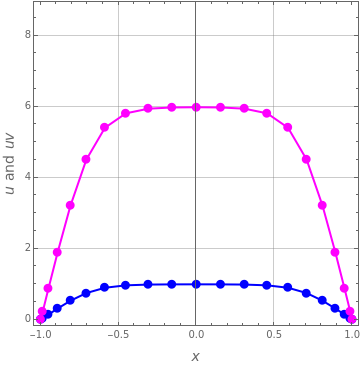
The steady-state temperature and reaction conversion along

y=0

are plotted in magenta and blue, respectively. You can vary the parameters

b

,

γ

, and

2

ϕ

as well as the number of Chebyshev collocation points,

N+1

.