Quantum Mechanics of a Bouncing Ball
Quantum Mechanics of a Bouncing Ball
The Schrödinger equation can be written , where is the mass of the ball (idealized as a point mass), is the acceleration of gravity, and is the vertical height (with ground level taken as ). For perfectly elastic collisions, the potential energy at can be assumed infinite: , leading to the boundary condition . Also, we should have as .
-ψ''(z)+mgzψ(z)=Eψ(z)
2
ℏ
2m
m
g
z
z=0
z=0
V(0)=∞
ψ(0)=0
ψ(z)0
z∞
The problem, as stated, is not physically realistic on a quantum level, given Earth's value of , because would have to be much too small. But an analogous experiment with a charge in an electric field is possibly more accessible. We will continue to refer to the gravitational parameters, however.
g
m
Redefining the independent variable as , the equation reduces to the simpler form . (The form of the variable is suggested by running DSolve on the original equation). The solution that remains finite as is found to be . (A second solution, , diverges as .)
x=z-
1/3
2g
2
m
2
ℏ
E
mg
ψ''(x)-xψ(x)=0
x∞
ψ(x)=constAi(x)
Bi(x)
x∞
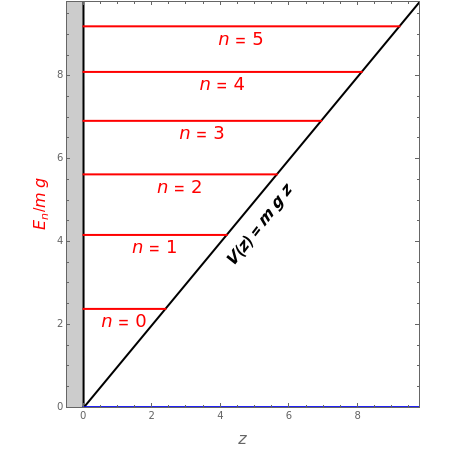
The eigenvalues can be found from the zeros of the Airy function: , using N[AiryAiZero[n]]. The roots lie on the negative real axis, the first few being approximately , , , , , , …. Defining the constant , the lowest eigenvalues are thus given by /mg=, /mg=4.08795, /mg=5.52056, and so on. The corresponding (unnormalized) eigenfunctions are (z)=Ai[α(z-/mg)]. These are plotted on the graphic.
E
n
Ai-=0
1/3
2g
2
m
2
ℏ
E
mg
-2.33811
-4.08795
-5.52056
-6.78671
-7.94413
-9.02265
α=
1/3
2g
2
m
2
ℏ
E
0
2.33811
-1
α
E
1
-1
α
E
2
-1
α
ψ
n
E
n