Pricing Put Options with the Crank-Nicolson Method
Pricing Put Options with the Crank-Nicolson Method
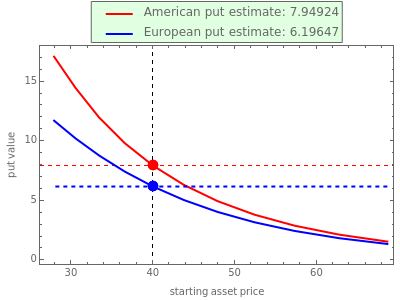
This Demonstration shows the application of the Crank–Nicolson (CN) method in options pricing. The CN method [1] is a central-time, central-space (CTCS) finite-difference method (FDM) for numerically solving partial differential equations (PDE). The CN scheme is the average of the implicit [2] and the explicit [3] schemes and can be used to numerically solve the Black–Scholes–Merton PDE [4, 5]. The CN scheme produces estimates of greater accuracy than either the explicit or implicit schemes.