Polynomial Atomic Functions for Fourier Analysis
Polynomial Atomic Functions for Fourier Analysis
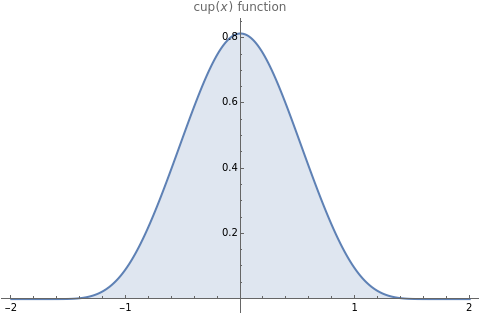
In computer terminology, an atomic process refers to a sequence of operations that can be executed by the CPU with a single instruction. (It has nothing to do with chemical atoms.) This Demonstration shows Fourier approximations (FA) of the family of polynomial atomic functions (pAF) and their Fourier transforms (spectrum). We consider a set of pAF, such as the functions , , , , , and , each of which is defined as a finite solution of a coordinate functional differential equation (FDE) [1, 2].
cup
fup
n
Ξ
n
up
m
ch
a,n
h
a
For example, the function is a solution of the FDE of advanced type, =((ax+1)-(ax-1)), where and the support of is . The FA of is (x,n,m)=+cos(πkx).
h
a
d
h
a
dx
2
a
2
h
a
h
a
a>1
h
a
-,
1
a-1
1
a-1
h
a
h
a
1
2
n
∑
k=1
m
∏
i=1
sin(k(a-1)π)
-i
2
k(a-1)π
-i
2
Here we use a FA technique to compute all the pAFs considered.