Pólya Vector Fields and Complex Integration along Closed Curves

integrand

f(z) =

1

z

curve to integrate over

C: z(t) =

t



, 0≤t≤2π

show

Pólya vector field

number of vectors displayed

55

scale factor for vector lengths

∫

C

1

z

dz

=

2π

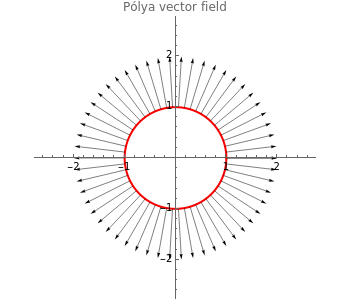
The Pólya vector field for a complex-valued function

u(x,y)+iv(x,y)

is the vector field

〈u(x,y),-v(x,y)〉

. This field is displayed along a curve, allowing for a visual interpretation of the complex integral. The real part of the complex integral is the same as the integral of the tangential flow, while the imaginary part is given by the integral of the normal flow.