Pieri's Ternary Relation and Euclidean Geometry
Pieri's Ternary Relation and Euclidean Geometry
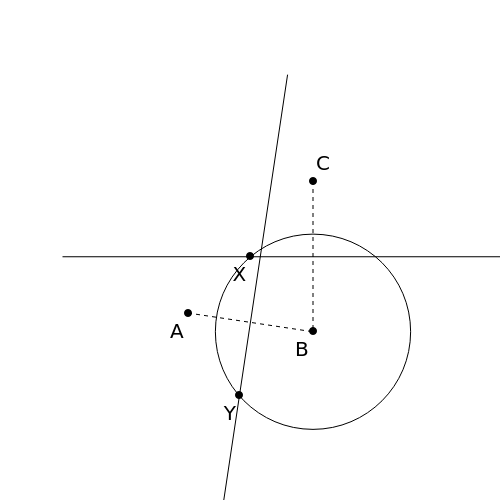
M. Pieri showed that the ternary relation of a point being equally distant from two other points (in symbols, ) can be used as the only primitive notion of Euclidean geometry of two or more dimensions [1]. This Demonstration shows Robinson's definition of the quartic relation
AB=BC
AB≤BC⇔∀X(BX=XC∃Y(AY=YB=BX))
in terms of Pieri's relation. This relation can be used to define relations that a point is between and ; that , , are collinear; and that is the midpoint of .
B
A
C
A
B
C
B
AC
You can drag the points shown as locators.