Phase Portrait and Field Directions of Two-Dimensional Linear Systems of ODEs
Phase Portrait and Field Directions of Two-Dimensional Linear Systems of ODEs
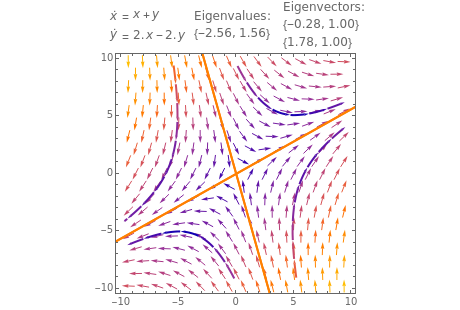
This Demonstration plots the phase portrait (or phase plane) and the vector field of directions around the fixed point of the two-dimensional linear system of first-order ordinary differential equations
(0,0)
x
a
1
b
1
y
a
2
b
2
Drag the four locators to see the trajectories of four solutions of the system that go through them. The position of these points can be chosen by clicking on wherever you like inside the graphics. Thick orange lines parallel to the eigenvectors are shown if the eigenvalues of the system are real.