Perturbation Theory in the de Broglie-Bohm Interpretation of Quantum Mechanics

time steps

50

perturbation factor Ω

0.05

superposition factor a

0.05

initialize

In the de Broglie–Bohm interpretation of quantum mechanics, the particle position and momentum are well defined, and the transition can be described as a continuous evolution of the quantum particle according to the time-dependent Schrödinger equation. There are no "quantum jumps." To study transitions in a two-level system, time-dependent perturbation theory must be used. These solutions are not exact solutions of the Schrödinger equation, but they are extremely accurate. For the particular case of a two-level system perturbed by a periodic external field (but without quantization of the transition-inducing field and ignoring radiation effects), an accurate solution can be derived (see Related Links).

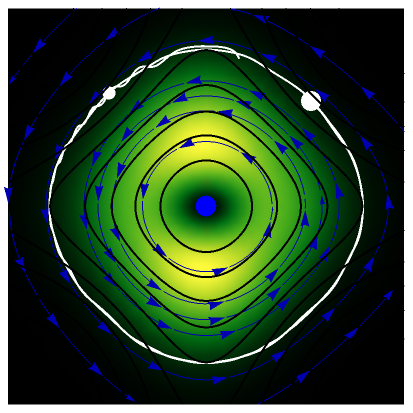
Here a very special transition is studied, which is a particle in a trigonometric two-dimensional Pöschl–Teller potential, where the transition goes from ground state

Θ

0,1

(x,y)

to a perturbed first excited superposition state

Θ

1,0

(x,y)+a

Θ

0,0

(x,y)

. Time-dependent transition effect in the Bohm approach was first described in [1]. This system is characterized by the fact that the trajectory varies between periodic and ergodic motion controlled by the factor

a

. In phase space during the quantum flow, the velocity exhibits two nodal points (vortices) and two saddle points, due to the singularities of the wavefunction, which leads to a chaotic motion in the configuration space. Chaos or ergodic motion emerges from the scattering process of the trajectory with the nodal points [2].