Permutations, Lehmer Code, and Lexicographic Index
Permutations, Lehmer Code, and Lexicographic Index
The number of ways to arrange seventeen objects in a row is , or for short. The arrangements are called permutations. Combinatorial theorists use five different notational systems for permutations.
17×16×15×14×13×12×11×10×9×8×7×6×5×4×3×2×1=355687428096000
17!
Assume that the objects are labeled by the numbers 1 to 17. The first notation has positions on top and the numbers of the rearranged objects on the bottom. It can be read as a mapping of a finite set of numbers, where the numbers on top get mapped to those below.
The second notation is just the bottom row of the first notation. (5 14 9 2 1 11 16 6 7 4 8 17 10 13 15 3 12) is a permutation.
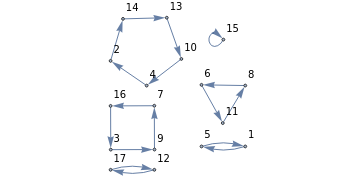
The third notation applies that mapping repeatedly to any starting number until there is a repetition. Then a new number is chosen to start the next cycle, and so on. (1 5)(2 14 13 10 4)(3 9 7 16)(6 11 8)(12 17)(15) is a cycle form. A permutation can be shown as a directed graph.
The fourth notation is the lexicographical index. The arrangement (5 14 9 2 1 11 16 6 7 4 8 17 10 13 15 3 12) is the hundred trillionth permutation if the permutations of 17 objects are sorted. Thus, 100000000000000 of 17! is a permutation.
The fifth notation is the Lehmer code, for example (4 12 7 1 0 6 9 2 2 1 1 5 1 2 2 0 0). The generating algorithm is basically "this number is greater than of the subsequent numbers." This is also known as the factorial number system representation of a number. Note that
n
10000000000000=4×16!+12×15!+7×14!+1×13!+0×12!+6×11!+9×10!+2×9!+2×8!+1×7!+1×6!+5×5!+1×4!+2×3!+2×2!+0×1!+0×0!
Gauss noted that every self-intersecting closed loop with crossings corresponds to a permutation by labeling every other intersection with 1 to . The reverse is not true, since permutations like (3 4 5 1 2) lead to nonplanar graphs.
n
n
Big numbers are needed to get to 27!, but in a slider, only =2147483648 discrete integer values are possible. Bigger numbers are split across sliders.
31
2