Periodic and Damped-Oscillatory Behavior of the Oregonator
Periodic and Damped-Oscillatory Behavior of the Oregonator
This Demonstration shows the oscillatory behavior of the Belousov–Zhabotinsky reaction (BZ reaction), which was modeled by Field, Körös, and Noyes (FKN) in the early 1970s. This is now known as the Oregonator model. It is based on the following mechanism:
A+Y→X+P
X+Y→2P
A+X→2X+2Z
2X→A+P
B+Z→fZ
1
2
where , , , , , and .
X=[]
HBrO
2
Y=[]
-
Br
Z=[Ce(IV)]
A=[Br]
-
O
3
B=[organicspecies]
P=[HOBr]
The law of mass action yields the following nondimensional 3×3 system of nonlinear ODEs:
ϵ=qy-xy+x(1-x)
dx
dτ
δ=-qy-xy+fz
dy
dτ
dz
dτ
where , , , and .
ϵ=0.0099
δ=2.4802×
-5
10
q=3.1746×1
-5
0
f∈[1.0,3.0]
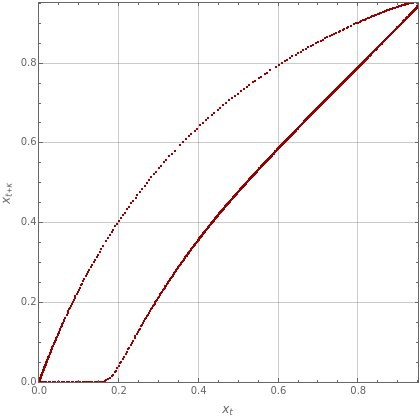
There is periodic behavior for , which is confirmed by (1) the sustained oscillations in the time series plot and (2) the limit-cycle in the time-delay reconstruction diagram (both plots are shown in red). This latter diagram is obtained by plotting versus with arbitrarily taken equal to 0.01. A transition occurs at approximately with time series exhibiting damped oscillation for (plot shown in blue) and the time-delay reconstruction diagram collapsing to a single blue point.
f≤2.41
x
t+κ
x
t
κ
f=2.42
f≥2.42