Penetration of Potential in a Semi-Infinite Region
Penetration of Potential in a Semi-Infinite Region
This Demonstration shows the penetration in a semi-infinite region of a dimensionless potential described by the model θ(ξ,τ)=θ(ξ,τ), θ(ξ,τ)=0, with the three boundary conditions: , , and , where is dimensionless distance, is dimensionless time, and Bi is the Biot number.
θ(ξ,τ)
∂
τ
∂
ξ,ξ
lim
ξ∞
θ(ξ,0)=0
θ(0,τ)=1
-θ(0,τ)=1
∂
ξ
θ(0,τ)-θ(0,τ)Bi=1
∂
ξ
ξ
τ
These classical problems are considered in many textbooks and in the booklet by M. D. Mikhailov and M. N. Özisik, Heat Transfer Solver, Englewood Cliffs, NJ: Prentice Hall, 1991. The potential could be temperature, concentration, etc., as described by M. D. Mikhailov and M. N. Özisik, Unified Analysis and Solutions of Heat and Mass Diffusion, New York: Dover, 1994.
For the case , the first animation was presented by Prof. U. Grigull at the opening of the Seventh International Heat Transfer Conference, Munich, FRG, September 6–12, 1982.
θ(0,τ)=1
In contrast to the existing animations, the frame ticks change with time , which conveniently lets you observe the potential distribution during penetration.
τ
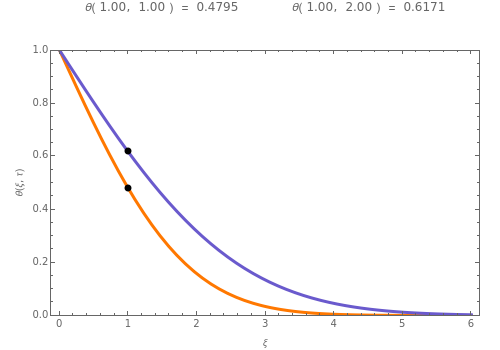
On the same plot are shown the dimensionless potentials (orange curve) and (blue curve) for two different materials with conductivities and related by the ratio .
θ(ξ,τ)
θ(ξ,τρ)
α
α
1
ρ=/α
α
1
For a fixed time , the slider determines black points on the two curves. The plot label gives the numerical values of followed by the numerical values of . Thus for any and the precise values of the potential are available.
τ
ξ
θ(ξ,τ)
θ(ξ,τρ)
τ
ξ
The slider for the Biot number Bi acts only in the case .
θ(0,τ)-θ(0,τ)Bi=1
∂
ξ