Particle in an Infinite Vee Potential
Particle in an Infinite Vee Potential
This Demonstration considers solutions of the Schrödinger equation for a particle in a one-dimensional "infinite vee" potential: , setting for simplicity. The solutions of the differential equation that approach zero as are Airy functions , as can be found using DSolve in Mathematica. The allowed values of are found by requiring continuity of at . The even solutions require , which leads to =, with , , , … being the first, second, third, … zeros of the Airy prime function: . The odd solutions have nodes , which leads to =, with , , , … being the first, second, third, … zeros of the Airy function: . The ground state is given by =0.808614.
-ψ''(x)+axψ(x)=Eψ(x)
1
2
ℏ=m=1
x±∞
ψ(x)=Ai(a|x|-E)
1/3
2
-2/3
a
E
ψ'(x)
x=0
n=0,2,4,…
ψ'(0)=0
E
n
-1/3
2
2/3
a
β
n
β
0
β
2
β
4
Ai'(-)=0
β
n
n=1,3,5,…
ψ(0)=0
E
n
-1/3
2
2/3
a
α
n
α
1
α
3
α
5
Ai(-)=0
α
n
E
0
2/3
a
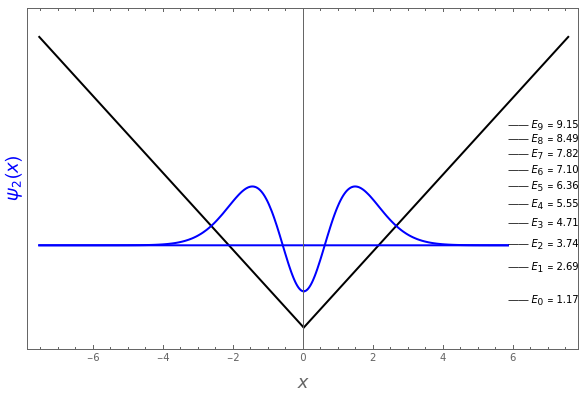
For user-selected and , the eigenfunctions (x)=Ai(a|x|-), with normalization constants =, are plotted as blue curves. The axis for each function coincides with the corresponding eigenvalue , the first ten values of which are shown on the scale at the right. The vertical scales are adjusted for optimal appearance.
n
a
ψ
n
N
n
1/3
2
-2/3
a
E
n
N
n
-1/2
2dx
∞
∫
0
2
Ai(ax-)
1/3
2
-2/3
a
E
n
x
E
n
A checkbox lets you compare the vee-potential eigenstates with the corresponding ones of the harmonic oscillator, drawn in red. The ground states of the two systems are chosen to coincide: =. The harmonic oscillator is more confining, so its eigenvalues are more widely spaced. For higher values of , the oscillator functions might move off scale.
E
0
1
2
ω
0
n