Packed Bed Reactor with Longitudinal Mixing
Packed Bed Reactor with Longitudinal Mixing
Consider an isothermal packed bed reactor (PBR) in which an irreversible first-order reaction is taking place. The reaction rate is given by , where is the rate constant and is the concentration of species . The reactor's length is . Assume that pure reactant enters at with a concentration . For a closed-closed vessel, the Danckwerts boundary conditions at the two ends of the reactor are and =0. The turbulent flow of the fluid in the pipe is characterized by the velocity . The concentration profile in this PBR is governed by the following partial differential equation:
A→B
r=kc
k
c
A
L
A
x=
-
0
c
0
c(x=)-==c(x=)
+
0
1
P
e
∂c
∂x
x=
+
0
c
0
-
0
∂c
∂x
x=L
u
c(x,t)
∂c
∂t
2
∂
∂
2
x
∂c
∂x
t≥0
0≤x≤L
where is a dispersion coefficient (expressed in /s), which takes into account longitudinal mixing in the pipe.
D
2
cm
Introduce the following dimensionless variables and parameters: =, =, =, , = (Péclet number), and =kτ (Damköhler number).
*
x
x
L
*
c
c
c
0
*
t
t
τ
τ=
L
u
P
e
uL
D
D
a
The dimensionless governing equation becomes:
∂
*
c
∂
*
t
1
P
e
2
∂
*
c
∂
2
*
x
∂
*
c
∂
*
x
D
a
*
c
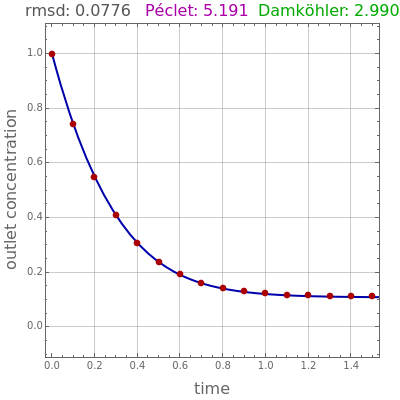
Assume that we have measured the outlet concentration of species using an appropriate analyzer (e.g. a refractometer). Such data, represented by the red dots in the figure, will have some white noise. This Demonstration estimates the two characteristic parameters of the reactor—the Péclet and the Damköhler numbers—by correlating the experimental data to the dispersion model. To do this, set values for and as well as the random noise level and let the Demonstration generate "experimental" data.
A
P
e
D
a
The fitted data is shown by the blue curve. The values of the parameters thereby determined are shown in magenta and green. Finally, the root-mean-square deviation (or rmsd, given in ) is computed. This computed value serves as an indication of the goodness of fit. As expected, the higher the noise level, the larger the rmsd (e.g. compare rmsd values in snapshots 2 and 3).
%