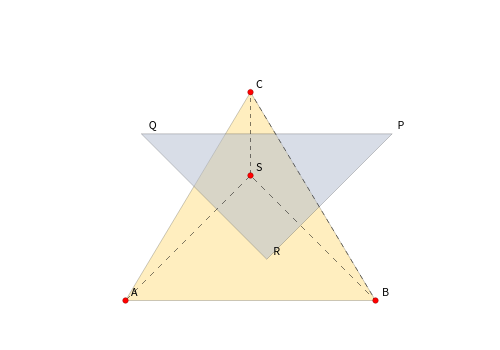
Orthologic Triangles
Orthologic Triangles
If and are such that the perpendiculars from the vertices of one to a corresponding side of the other are concurrent at a point , we say that the two triangles are orthologic. (Regard a side as extending infinitely in both directions.) Using the labeling shown, this means that the perpendiculars from to , from to , and from to are concurrent. In 1827, Steiner discovered that this relation is symmetric. That is, if the perpendiculars from to , from to , and from to are concurrent, then the perpendiculars from to , from to , and from to are also concurrent. Drag the red disks to move the points , , , and . There are also three sliders to modify the sides of .
△ABC
△PQR
S
A
QR
B
RP
C
PQ
A
QR
B
RP
C
PQ
P
BC
Q
AC
R
AB
A
B
C
S
△PQR