Optimal Temperature Policy for a Reversible Reaction
Optimal Temperature Policy for a Reversible Reaction
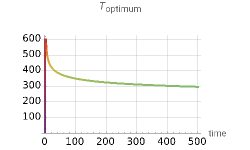
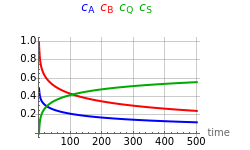
This Demonstration shows the temperature trajectory that maximizes the reaction rate of a reversible reaction.
For the reaction
A+B⇌Q+S
r
A
A
1
-/RT
E
1
e
2
c
A0
x
A
x
A
A
2
E
2
e
2
c
A0
2
x
A
with and ==0,
M=
c
B0
c
A0
c
Q0
c
S0
where and are the pre-exponential Arrhenius constants for the forward and reverse reactions, and are the energies of activation, is the universal gas constant, is the absolute temperature, , , , and are the initial concentration of the reactants, and is the conversion of species . The temperature function that gives the maximum reaction rate satisfies the condition =0 at each point in time; this function has an analytical solution for this reaction [1]
A
1
A
2
E
1
E
2
R
T
c
A0
c
B0
c
Q0
c
S0
x
A
A
∂
r
A
∂T
T
optimum
-1
-ln()
1
B
1
B
2
B
3
with
B
1
E
1
E
2
R
B
2
A
2
E
2
A
1
E
1
B
3
2
x
A
(1-)(M-)
x
A
x
A
the initial concentrations of and are taken equal to 0.5, and 1.0.
A
B
One complication can occur: for low conversions, may have a value sufficiently small enough to make ≤1; then the equation for gives a value →∞ (or negative); in practice the temperature is limited by the reactor materials or the catalyst's physical properties. The optimum temperature profile and the concentration of the reactants as a function of time are shown for user-set values of reaction time, maximum allowable temperature, and parameters and .
B
3
B
2
B
3
T
optimum
T
optimum
B
1
B
2