Optimal Setup of Two Continuous Stirred-Tank Reactors (CSTRs) in Series
Optimal Setup of Two Continuous Stirred-Tank Reactors (CSTRs) in Series
ManipulateModule{plt,V,Area,X0,CA0,f,Areaf},CA0=1;f[X_]:=(0.2+CA0(1-X))(CA0(1-X));Area=(f[0.9]-f[X])(X-0);V=10((X-0)f[X]+(0.9-X)f[0.9]);Areaf[X_]:=(f[0.9]-f[X])(X-0);X0=X/.FindRoot[D[Areaf[X],X]0,{X,0.5}];plt=Plotf[X],{X,0,1},PlotStyle{Red,Thick},FrameTrue,FrameLabel"conversion","",PlotRange{{0,1},{0,5}},ImageSize{500,350},AxesOrigin{0,0};TabView[{"trial & error"Show[plt,Graphics[{Opacity[0.4],Brown,Rectangle[{0,0},{X,f[X]}]}],Graphics[{Opacity[0.4],Red,Rectangle[{0,f[X]},{X,f[0.9]}]}],Graphics[{Opacity[0.4],Green,Rectangle[{X,0},{0.9,f[0.9]}]}],Graphics[Style[Text["total volume = "<>ToString[SetPrecision[V,4]],{0.2,4},{-1,0}],Black,Bold,14]],Graphics[Style[Text["total red shaded area = "<>ToString[SetPrecision[Area,4]],{0.2,3.6},{-1,0}],Black,Bold,14]]],"exact solution"Show[plt,Graphics[{Opacity[0.4],Brown,Rectangle[{0,0},{X0,f[X0]}]}],Graphics[{Opacity[0.4],Red,Rectangle[{0,f[X0]},{X0,f[0.9]}]}],Graphics[{Opacity[0.4],Green,Rectangle[{X0,0},{0.9,f[0.9]}]}],Graphics[Style[Text["total volume = "<>ToString[SetPrecision[10((X0-0)f[X0]+(0.9-X0)f[0.9]),4]],{0.2,4},{-1,0}],Black,Bold,14]],Graphics[Style[Text["volume of first reactor= "<>ToString[SetPrecision[10((X0-0)f[X0]),4]],{0.2,2.8},{-1,0}],Black,Bold,14]],Graphics[Style[Text["volume of second reactor = "<>ToString[SetPrecision[10((0.9-X0)f[0.9]),4]],{0.2,2.4},{-1,0}],Black,Bold,14]],Graphics[Style[Text["conversion after first CSTR = "<>ToString[SetPrecision[X0,4]],{0.2,3.2},{-1,0}],Black,Bold,14]],Graphics[Style[Text["total red shaded area = "<>ToString[SetPrecision[Areaf[X0],4]],{0.2,3.6},{-1,0}],Black,Bold,14]]]},Dynamic[tab]],{{X,0.5,"conversion after first CSTR"},0,0.89,0.005,Appearance"Labeled",Enabledtab===1},{{tab,2},{1,2},ControlTypeNone},TrackedSymbols{X,tab}
-1
r
A
Consider the reaction , with the kinetics .
AR
-=
r
A
c
A
0.2+
c
A
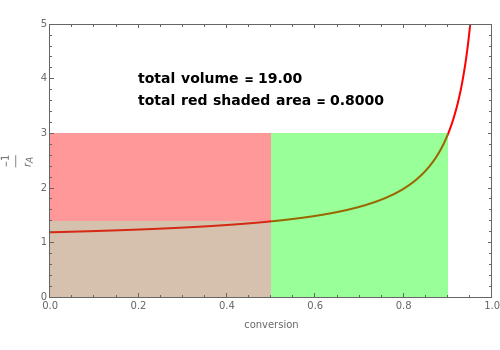
A liquid feed to two CSTRs in series, containing 1 mol A/liter, has a flow rate equal to 10 liter/minute. The required exit conversion is 90%. This Demonstration finds the total volume of the two reactors for various values of the conversion after the first CSTR. The best setup, which minimizes the total volume of the two reactors, can be found by trial and error by changing the value of the conversion after the first CSTR. An exact solution, obtained by maximizing the area of the red shaded rectangle, can be found and is given by this Demonstration. This solution shows that for reactions with order less than one, the first reactor must be larger than the second. If the reaction order were greater than one, the inverse would be true (the reactor with the larger volume is the second reactor). For first-order reactions, the ideal setup is when both reactors have the same volume.