One-Soliton Nonlinear Schrödinger Equation with Arbitrary Linear Time-Dependent Potential
One-Soliton Nonlinear Schrödinger Equation with Arbitrary Linear Time-Dependent Potential
This Demonstration considers the nonlinear Schrödinger equation, also known as the Gross–Pitaevskii equation. This pertains to an arbitrary linear time-dependent potential in the causal interpretation for a bright one-soliton solution, equivalent to the dynamics of a soliton solution in one-dimensional Bose–Einstein condensate. The existence of soliton solutions is a general feature of nonlinear wave equations, to which this trajectory concept is applied.
The causal interpretation of quantum theory developed by Louis de Broglie and David Bohm introduced trajectories that are guided by a quantum potential. The velocities of single particles, following the trajectories, are determined by the phase of the wavefunction. The system is time reversible.
Despite the problems of the trajectory concept in quantum theory, the causal interpretation introduces a particle-based theory in the nonlinear wave mechanics naturally. The time evolution of the position could be interpreted as streamlines of the wave or as idealized test particles that do not interact on each other and do not perturb the wave.
x(t)
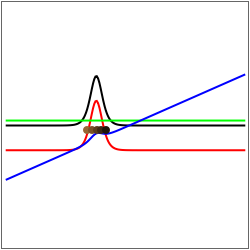
In the graphic on the left, you can see the position of the particles, the squared wavefunction (black), the effective potential term (blue), the quantum potential (red), and the velocity (green). On the right, the graphic shows the squared wavefunction, as well as the trajectories.