WOLFRAM NOTEBOOK

WOLFRAM|DEMONSTRATIONS PROJECT

One-Dimensional Heat Conduction with Temperature-Dependent Conductivity

trial solution order

exact and trial solutions

trial solution:1.32624x-0.326238

Consider the following nonlinear boundary value problem

k(T)

, with

T(z=0)=

T(z=d)=

, and

0≤z≤d

. This equation with the boundary conditions (BCs) describes the steady-state behavior of the temperature of a slab with a temperature-dependent heat conductivity given by

k(T)=

+α(T-

)

Introducing nondimensional temperature and position using

θ=

T-

and

, the governing equation and BCs become

(1+aθ)

dθ

, with

a=α/

θ(x=0)=0

, and

θ(x=1)=1

. Without loss of generality, set

a=1

. Then this problem admits an analytical solution given by

θ(x)=-1+

1+3x

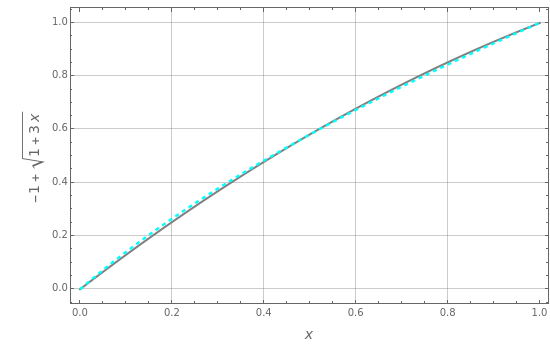
We use Galerkin's method to find an approximate solution in the form

(x)=x+

∑

i=1

(

i+1

-x)

. The unknown coefficients

of the trial solution are determined using the residual

,x)=(1+a

(x))

and setting the integrals

∫

,x)(

-x)dx=0

for

j=2,…,N+1

. You can vary the order of the trial solution,

N+1

. The Demonstration plots the analytical solution (in gray) as well as the approximate solution (in dashed cyan). The polynomial expression of the trial solution is displayed on the same plot. In addition, the difference between the exact and approximate solutions,

e(x)

, is plotted. This error is seen to decrease as the order of the trial solution,

N+1

, is increased.

You are using a browser not supported by the Wolfram Cloud

Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.

I understand and wish to continue anyway »