Octonions and the Fano Plane Mnemonic
Octonions and the Fano Plane Mnemonic
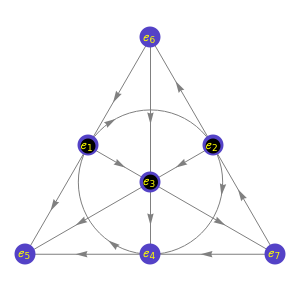
Octonions form an eight-dimensional noncommutative, nonassociative normed division algebra. Octonions have seven imaginary units whose multiplication table can be encoded using the Fano plane mnemonic, shown here as a directed graph. The product of two distinct units equals the unique unit such that the three units form three immediately connected vertices of the graph, multiplied by the signature of the permutation that orders the three vertices in the graph.
ℯ
k
For any three octonions , and the associator is . The associator measures the nonassociativity of the octonions. Select triples of octonionic units to compute their associator. Observe that their associator vanishes on immediately connected triples of octonionic units. Such triples, together with the unit element, form the quaternionic subalgebras of octonions.
a
b
c
(a⊙b)⊙c-a⊙(b⊙c)