Numerical Solution of the Advection Partial Differential Equation: Finite Differences, Fixed Step Methods
Numerical Solution of the Advection Partial Differential Equation: Finite Differences, Fixed Step Methods
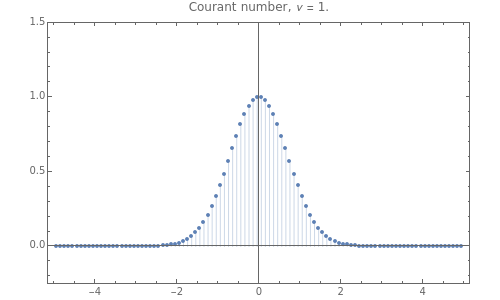
This Demonstration shows some numerical methods for the solution of partial differential equations: in particular we solve the advection equation. We use finite differences with fixed-step discretization in space and time and show the relevance of the Courant–Friedrichs–Lewy stability criterion for some of these discretizations.