Nonisothermal Effectiveness Factor (The Weisz and Hicks Problem)
Nonisothermal Effectiveness Factor (The Weisz and Hicks Problem)
Consider a nonisothermal first-order reaction taking place in a spherical catalyst pellet. These are the governing equations, obtained from mole and enthalpy balances, and the boundary conditions, obtained from the symmetry condition and the known values of concentration and temperature at the surface:
AB
d
dr
2
r
D
A
d
c
A
dr
2
r
c
A
d
dr
2
r
dT
dr
2
r
c
A
d
c
A
dr
dT
dr
c
A
c
AS
T(r=R)=
T
S
where is the radius of the spherical pellet, is the effective thermal conductivity of the pellet, is the reaction rate constant, is the effective binary diffusivity of within the pellet, is the heat of reaction, is the concentration, and is the temperature. is the radial position, and are the concentration and temperature at the surface of the catalyst pellet (i.e. at where is the radius of the spherical catalyst pellet).
R
λ
k
D
A
A
ΔH
c
A
T
r
c
AS
T
S
r=R
R
The rate constant is a function of temperature: .
k(T)=k()exp-1
T
S
-
E
a
R
T
S
T
S
T
In terms of dimensionless quantities, we have the following boundary value problem:
d
dξ
2
ξ
d
ϕ
A
dξ
2
ξ
2
Φ
γβ(1-)
ϕ
A
1+β(1-)
ϕ
A
ϕ
A
ϕ
A
ϕ
A
where and =(r).
ξ=
r
R
ϕ
A
c
A
c
AS
Three dimensionless parameters are introduced in the new governing equation:
Φ=R
k()
T
S
D
A
β=-ΔH
D
A
c
AS
λ
T
S
γ=
E
a
R
T
s
Φ
Φ<<1
γ
γ
The Demonstration displays the effectiveness factor (red curve) , a measure of the of the total reaction rate inside the pellet compared to its value at the pellet surface, versus the Thiele modulus , for various values of parameter .
η
Φ
β
The effectiveness factor is given by the formula
R
tot
R
∫
0
c
A
2
r
4
3
3
R
T
S
c
AS
where .
η=3(ξ)expdξ
1
∫
0
ϕ
A
γβ(1-(ξ))
ϕ
A
1+β(1-(ξ))
ϕ
A
2
ξ
The solution is based on the arc length continuation method and the Chebyshev orthogonal collocation technique (with collocation points). For large values of and for , our method performs poorly and we use the fact that the effectiveness factor is inversely proportional to the Thiele modulus (see blue dashed line).
N+1=41
Φ
β≥0.24
η
Φ
The parameter , which you can set, is a measure of the relative importance of the heat of reaction to conduction.
β
Large values of mean that there is significant internal heating; thus for the effectiveness factor will be greater than 1. This means that the rate of reaction is higher inside the pellet compared to its value at the surface of the pellet in the absence of internal diffusion resistance.
β
Φ≈1
Negative values of the parameter correspond to endothermic reactions () and smaller values of the effectiveness factor .
β
ΔH>0
η
When , the internal transport resistance becomes large (a depleted zone inside the pellet forms and the concentration of species is low). Thus, the reaction rate inside the pellet is smaller than its value at the pellet surface and consequently the effectiveness factor becomes very small compared to 1.
Φ≫1
A
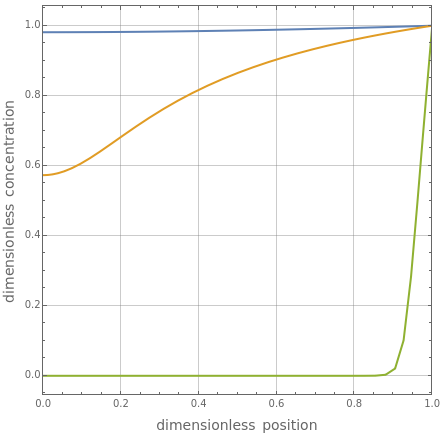
The Demonstration also plots the dimensionless concentration and the dimensionless temperature (given by ) versus the dimensionless position . As shown in the first two snapshots, up to three solutions can exist for a certain range of values of the Thiele modulus.
ϕ
A
T/=1+β(1-)
T
s
ϕ
A
ξ=
r
R