Natural Convection between Two Vertical Plates

Grashov number

1.

ξ

-1.

The dimensionless vertical velocity

V=vd/ν

inside two vertical plates at distance

2d

and temperatures

T

1

and

T

2

is computed for specified Grashov number

Gr=g

3

d



2

ν

β(

T

2

-

T

1

)

, where

v

is the velocity

m/s

,

d

is the distance in meters,

ν

is the kinematic viscosity in

2

m

/s

,

g

is the gravitational acceleration in

m/

2

s

, and

β

is the volumetric coefficient of thermal expansion in

o

-1

K

.

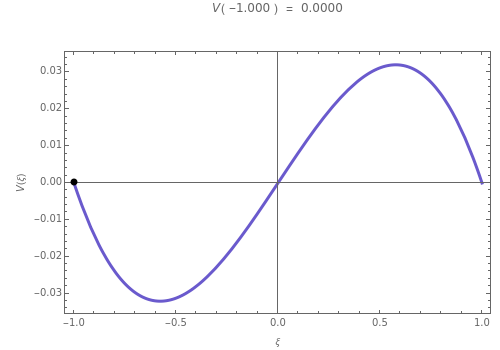
For a fixed Grashov number,

ξ

determines black points on the curve, followed by the numerical values of

V(ξ)

. Thus for any

Gr

and

ξ

the precise values of the velocity are available.

The frame ticks change with Grashov number

Gr

, which conveniently lets you observe that the shape of the velocity distribution did not change.