Motion of a Simple Pendulum with Damping
Motion of a Simple Pendulum with Damping
This Demonstration shows the motion of a pendulum obeying a classical pendulum differential equation with damping proportional to its angular velocity.
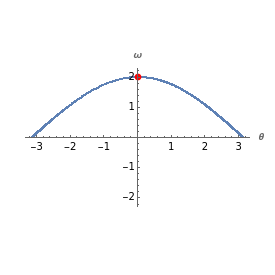
The visualization contains an approximate solution to the simple pendulum equation (with damping) θ=-ksin(θ)-αθ, where is the pendulum angle, is time, is a length parameter, and is a damping factor. The diagram on the left is a phase portrait of the system, where the horizontal axis is the angle of the pendulum and the vertical axis is the angular velocity.
∂
t,t
∂
t
θ
t
k
α