WOLFRAM NOTEBOOK

WOLFRAM|DEMONSTRATIONS PROJECT

Morphing Cartesian to Polar Coordinates

​
convert
r=3cos(θ)
r=3sin(θ)
r=cos(θ)+1
r=sin(θ)+1
r=2cos(θ)+1
r=2sin(θ)+1
r=3sin(2θ)
r=3cos(2θ)
r=2cos(3θ)+1
r=cos(5θ)+2
r=θ
r=θ/2
r=3
r constant
θ constant
black background
colored points
axes
radian ticks
large points
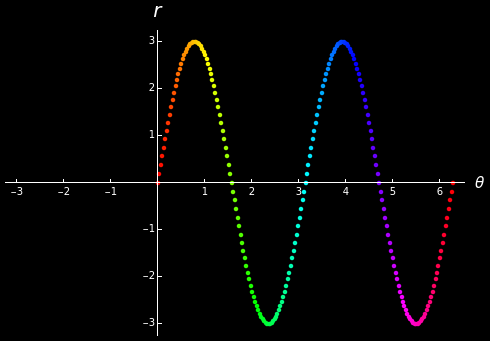
This Demonstration helps you visualize how a rectangular graph becomes a polar graph. Given a function
r=f(θ)
, each point
(r,θ)
is initially graphed in a
θ
-
r
plane using a rectangular coordinate system. The points are then moved along linear paths to their corresponding polar locations in the
x
-
y
plane. Colors help indicate which points end up where and how the relative extrema become extrema in the polar graph. Constant
r
and constant
θ
illustrate how the rectangular grid becomes a polar grid.
Wolfram Cloud

You are using a browser not supported by the Wolfram Cloud

Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.


I understand and wish to continue anyway »

You are using a browser not supported by the Wolfram Cloud. Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.