Method of Images in Electrostatics
Method of Images in Electrostatics
The potential of a point charge in the neighborhood of a grounded conductor is given by a solution of Laplace's equation ϕ=0, subject to the boundary condition that on the surface of the conductor. This solution is unique in the region enclosed by the conductor. Adding charges outside that region, which reproduce the same boundary conditions, can alternatively lead to a valid solution to the original problem. Under certain favorable conditions, it is possible to apply the method of images, in which one or more image charges of specified magnitude can be strategically placed to enable the Laplace equation with the given boundary conditions to be more easily solved.
2
∇
ϕ=0
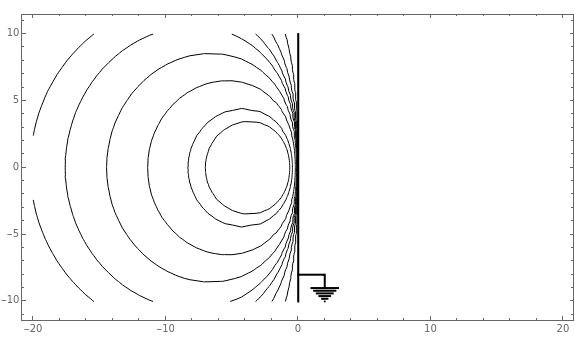
Two classic examples are considered in this Demonstration. A point charge located at near an infinite grounded plane conductor at has the same potential distribution as a pair of charges and symmetrically placed with respect to the plane. The potential is then given by . The labeled equipotentials in the contour plot can be multiplied by to give their actual values. A point charge at either inside or outside a grounded spherical conductor of radius , centered at the origin, can be solved by placing an image charge --q at .
q
r
0
x=0
q
-q
ϕ(r)=-
q
4π
ϵ
0
1
|r-|
r
0
1
|r+|
r
0
q
4π
ϵ
0
q
r
0
r
q'=
r
||
r
0
r'=
2
r
2
(|)
r
0
r
0
You can drag the point charge , a locator. A checkbox enables you to see the image charge . It will go off-scale if the locator is too close to the center of the sphere, but it still contributes to the potential.
q
q'