Maximum Entropy Probability Density Functions

constraints

specified μ and

2

σ

specified μ

μ

0.5

σ

0.01

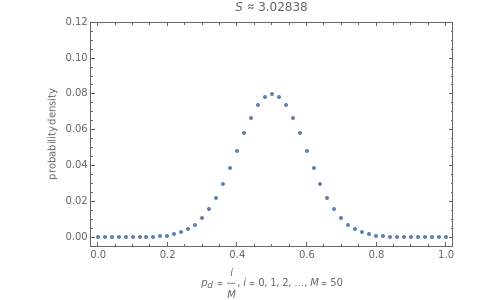
The principle of maximum entropy can be used to find the probability distribution, subject to a specified constraint, that is maximally noncommittal regarding missing information about the distribution. In this Demonstration the principle of maximum entropy is used to find the probability density function of discrete random variables defined on the interval

(0,1)

subject to user-specified constraints regarding the mean

μ

and variance

2

σ

. The resulting probability distribution is referred to as an

A

p

distribution [1]. The mean of the

A

p

distribution associated with a proposition

A

is the probability of that proposition, and the variance of the

A

p

distribution is a measure of the amount of confidence associated with predicting the probability of the proposition. When only the mean is specified, the entropy

S

of the

A

p

distribution is maximal when the specified mean probability is

μ=0.5.

When both mean and variance are specified, the entropy

S

of the

A

p

distribution decreases as the specified variance decreases.