Markov Chain Monte Carlo Simulation Using the Metropolis Algorithm

proposal σ

random seed

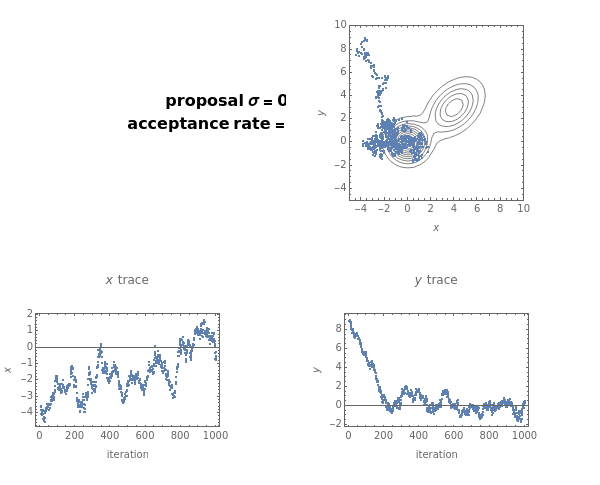
This Demonstration allows a simple exploration of the Metropolis algorithm sampling of a two-dimensional target probability distribution as a function of the width (sigma) of a circularly symmetric Gaussian proposal distribution. If the sigma is too small almost all proposals are accepted, the samples are highly correlated, and the burn-in period is long. If the proposal sigma is too large, hardly any proposals are accepted, and the sampling sticks. When a proposal is not accepted the new sample is just a repeat of the previous sample. Somewhere in between, the samples are minimally correlated and efficiently concentrate in regions where the target probability distribution is significant.

The Demonstration produces three graphs. In the first the dots show the individual Metropolis samples in (

x

,

y

). The true target probability distribution is shown by the blue contours. The proposal sigma is given on the left along with the proposal acceptance rate expressed as a percentage. The second and third graphs show the individual samples in the

x

and

y

parameters. For small values of the proposal sigma, the burn-in period is sometimes longer than the simulation.