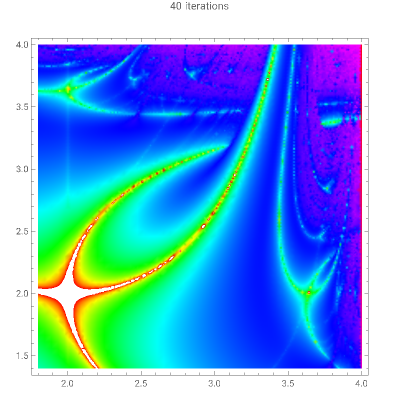
Lyapunov Fractals
Lyapunov Fractals
The algorithm for computing the fractal is summarized as follows:
1. Choose a string of A’s and B’s of any nontrivial length (e.g., AABAB).
2. Construct the sequence formed by successive terms in the string, repeated as many times as necessary.
S
3. Choose a point .
(a,b)∈[0,4]×[0,4]
4. Define the function =a if =A, and =b if =B.
r
n
S
n
r
n
S
n
5. Let =0.5, and compute the iterates =(1-).
x
0
x
n+1
r
n
x
n
x
n
6. Compute the Lyapunov exponent: . In practice, is approximated by choosing a suitably large (in the Manipulate code, the variable “iterations” corresponds to ).
λ=log=log(1-2)
lim
N∞
1
N
N
∑
n=1
x
n+1
x
n
lim
N∞
1
N
N
∑
n=1
r
n
x
n
λ
N
N
7. Color the point according to the value of obtained.
(a,b)
λ
8. Repeat steps 3–7 for each point in the image plane.