Locus of the Center of a Circle Inscribed in a Circular Segment

base line

0.2

position

0.1

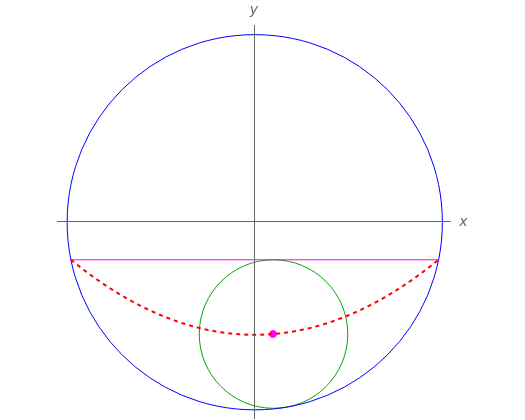
The trajectory of the center of a moving circle inscribed in a circular segment is parabolic.

This Demonstration shows this result with a horizontal chord ("base line").

Proof: Let

C

be a circle with its center at the origin and radius

R

with a horizontal chord

L

given by

y=b

and let

D

be the small circle inscribed on the circular segment bounded by

C

and

L

. Since the circles

C

and

D

are tangent, the tangent point and the centers of the circles are collinear. Let

(x,y)

be the coordinates of the center of

D

. The radius of

D

is equal to

y-b

. Hence the distance from the origin to the center of

D

is

1/2



2

x

+

2

y



=R-(y-b)

, which is the equation of a parabola.