Kim's Method for Pricing American Options
Kim's Method for Pricing American Options
This Demonstration shows Kim's method [1] for pricing American options. A European financial option is an instrument that allows its holder the right to buy or sell an equity at a future maturity date for a fixed price called the "strike price." An American option allows its holder to exercise the contract at any time up to the maturity date, and because of this it is worth more than the European option, by an amount called the "early exercise premium." For the American call's holder, the early exercise becomes optimal when the underlying asset price exceeds a critical boundary , above which the intrinsic value of the option becomes greater than its holding value.
*
B
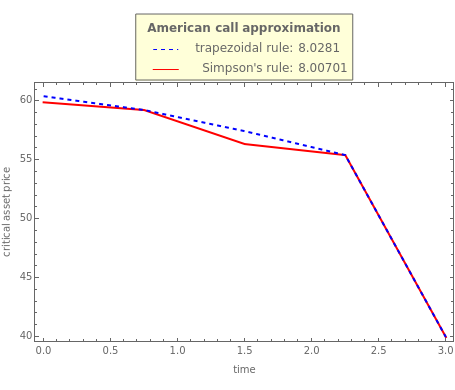
According to Kim's method, the valuation of the American option derives from an integral expression of the early exercise premium as a function of the optimal exercise boundary plus the value of the European option. The plot shows the optimal boundary approach, using either the trapezoidal rule (blue dashed line) or Simpson's rule (red line) to approximate the early exercise premium integral. Both approximation techniques use the same time discretization (from 4 to 50 time steps). The table shows the American call price depending on the integral approximation technique and time discretization.
*
B