How the Zeros of the Zeta Function Predict the Distribution of Primes

start x axis at (from 0 to 400)

0

length of x axis (from 10 to 100)

30

pairs of zeta zeros (from 0 to 100)

0

always show Riemann's R(x)

display π(x) values in a tooltip

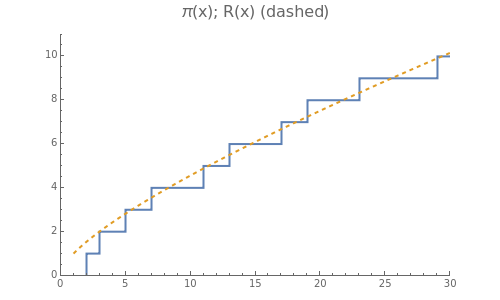
In number theory,

π(x)

is the number of primes less than or equal to

x

. Primes occur seemingly at random, so the graph of

π(x)

is quite irregular. This Demonstration shows how to use the zeros (roots) of the Riemann zeta function

ζ(s)

to get a smooth function that closely tracks the jumps and irregularities of

π(x)

. This illustrates the deep connection between the zeros of the zeta function and the distribution of primes.