Heisenberg Uncertainty Product for Different Photon States
Heisenberg Uncertainty Product for Different Photon States
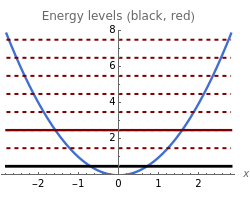
Each mode of the quantized radiation field can be associated with a quantized harmonic oscillator. This Demonstration shows the dependence of Heisenberg's uncertainty product (for momentum and position ), on the quantum number , when the oscillator has the energy eigenstate (in units of ). The integer denotes the energy and the number of photons in the radiation mode, . The uncertainty product is an increasing function of . The minimal product is valid for the energy ground state, , represented by black lines in the diagrams.
p
q
ΔpΔq=(2n+1)
ℏ
2
n
|n>
ℏ
2
n
n=0,1,2,…
n
ΔpΔq=
ℏ
2
n=0
In contrast to a state with a definite number of photons, a coherent state is defined in quantum optics as an eigenstate of the photon annihilation operator , , where is complex valued. The radiation of a single mode laser represents such a state; each coherent state has the minimum-uncertainty product allowed by quantum physics, . Therefore, coherent states provide the closest quantum mechanical analog to a classical single-mode field. These are not shown in this Demonstration.
|α>
a
a|α>=α|α>
α
ΔpΔq=
ℏ
2