Heisenberg Group Action on Quintics

polynomial coefficients

c

1

-5

c

2

-5

c

3

-5

c

4

-5

c

5

-5

c

6

-5

linear functionals

λ

-2

operators

y

-5

d

-5

z

-5

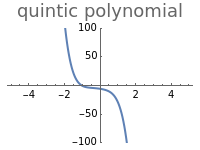
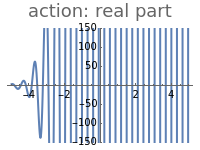
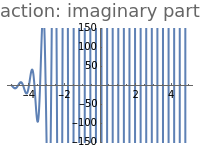
This Demonstration shows the action of the Heisenberg group on a family of quintic polynomials with compact support. The Heisenberg group is a nilpotent Lie group that has a natural action on the vector space of square integrable functions on the real line. In representation theory and quantum mechanics such actions belong to the Schrödinger representation. Let

H

be the Heisenberg group and

(z,y,d)∈H

. Schrödinger representations of type

π

λ

are in one-to-one correspondence with a family of linear functionals of the Lie algebra of

H

parametrized by

(λ,0,0)

, where

λ∈

*



. If

f

is square-integrable,

π

λ

(z,y,d)f(t)=

λz

e

-iλyt

e

f(t-d)

. Such actions are simply a combination of modulations and translations.