Heat Transfer and the Second Law of Thermodynamics
Heat Transfer and the Second Law of Thermodynamics
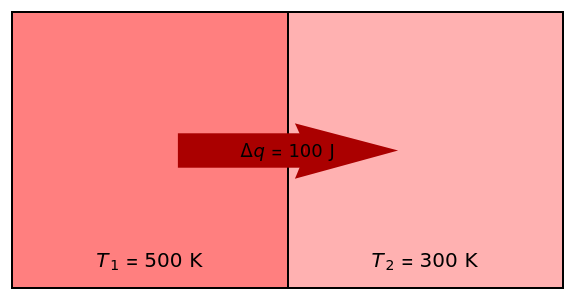
Two thermal reservoirs at the same temperature, =, can, in concept, exchange an increment of heat in either direction. Since it can just as easily flow in the opposite direction, this represents what is known as a reversible process and can be designated . By convention, is positive if heat flows into a reservoir and negative () if it flows out. When >, it is a matter of experience that flows spontaneously (or irreversibly) from the hotter to the cooler reservoir. One can still set if one conceptualized an infinite number of intermediate reservoirs at temperature increments varying infinitesimally between and .
T
2
T
1
Δq
Δq
Δ
q
rev
Δq
-Δq
T
2
T
1
Δq
Δq=Δ
q
rev
T
2
T
1
An increment represents the process of heat exchange between two systems. Neither system can be said to possess a quantity of heat . In the usual terminology, is not a "function of state" for a thermodynamic system. However, turns out to represent the differential of a new function of state, , where is known as the entropy. A derivation of this relation is given in Details for the case of an ideal gas.
Δq
q
q
d/T
q
rev
dS
S
A compact statement of the second law of thermodynamics is that the entropy of an isolated system (or of the whole universe) always increases in a spontaneous process, . The reverse process is unattainable—as Bertrand Russell put it, "You cannot unscramble eggs." The limiting case pertains to reversible processes (themselves an idealization).
ΔS>0
ΔS=0
An operational statement of the second law is due to Clausius: "It is impossible in a cyclic process to produce no other effect than the transfer of heat from a cooler to a warmer body." Of course, refrigerators do this all the time, but this requires coupling to other devices, such as motors and condensers.
In this Demonstration, you can vary the temperatures and and the quantity of heat transferred, . The total entropy change of the system is then calculated using . Recall that is counted as negative when a reservoir gives off heat. The system of two reservoirs is presumed to be isolated from its surroundings.
T
2
T
1
Δq
ΔS=+
Δ
q
1
T
1
Δ
q
2
T
2
Δq