Harmonic-Gaussian Double-Well Potential

α

2

β

5

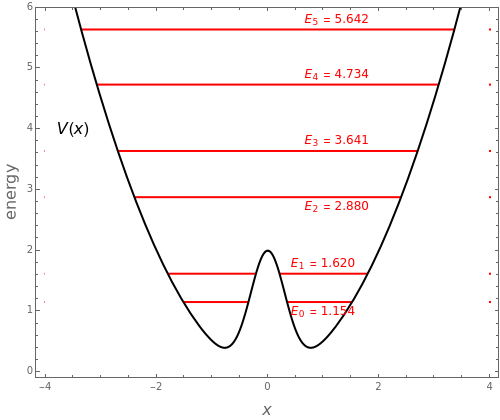
A variant of a double-well potential is a harmonic oscillator perturbed by a Gaussian, represented by the potential

V(x)=

1

2

k

2

x

+α

-β

2

x

e

. A similar function was used to model the inversion of the ammonia molecule [1]. The problem can be treated very efficiently using second-order perturbation theory based on the unperturbed harmonic oscillator. The first six energy levels are computed here.

The unperturbed Hamiltonian is

(0)

H

=-

2

ℏ

2μ

2

d

2

x

+

1

2

k

2

x

. For convenience, we set

ℏ=μ=k=1

. The unperturbed eigenfunctions are given by

ϕ

n

(x)=

-1/2

(

n

2

n!

π

)

H

n

(x)

-

2

x

2



, where

H

n

(x)

are Hermite polynomials. The unperturbed eigenvalues are then

(0)

E

n

=n+

1

2

,n=0,1,2,…

. The perturbation is the Gaussian function

(1)

H

=β

-α

2

x

e

. To second-order in perturbation theory, we have

E

n

=

(0)

E

n

+

(1)

H

n,n

+

∞

∑

k≠n=0

(1)

H

n,k

(1)

H

k,n

(0)

E

n

-

(0)

E

k

. (In practice, the sum is truncated at some

n

max

).

When

α=0

, the perturbation reduces to zero and the system reverts to a simple harmonic oscillator. As the central barrier becomes wider, the lower eigenvalues (

n=0

and

n=1

; also

n=2

and

n=3

) approach degenerate pairs. The situation becomes similar to tunneling, giving two eigenstates of opposite parity, with their linear combinations approximating localized states.