Gram-Schmidt Process in Two Dimensions

●

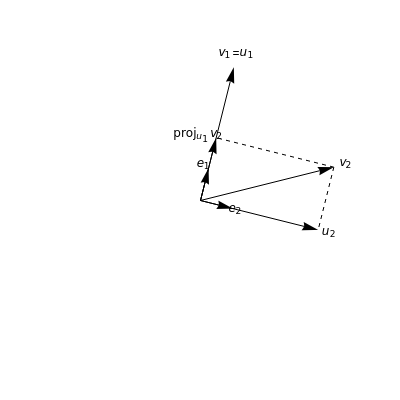
The Gram-Schmidt process is a means for converting a set of linearly independent vectors into a set of orthonormal vectors. If the set of vectors spans the ambient vector space, then this produces an orthonormal basis for the vector space.The Gram-Schmidt process is a recursive procedure. After the first

k-1

vectors have been converted into

k-1

orthonormal vectors, the difference between the

th

k

original vector and its projection onto the space spanned by the first

k-1

orthonormal vectors is normalized to obtain the

th

k

vector in the orthonormal collection.In two dimensions, start with a vector

v

1

=

u

1

and normalize it to obtain

e

1

=

v

1

||

v

1

||

. Next, project

v

2

onto

v

1

and compute

u

2

, the difference between

v

2

and this projection. Finally, normalize this vector to obtain

e

2

.