Generalized Extreme Value Distributions: Application in Financial Risk Management
Generalized Extreme Value Distributions: Application in Financial Risk Management
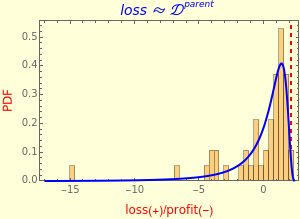
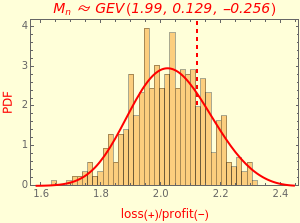
This Demonstration illustrates the Fisher–Tippett–Gnedenko theorem in the context of financial risk management. A sample of observations is drawn from a parent distribution that describes the probability of historical losses of a portfolio (left-hand plot). A number of draws () are repeated to obtain a histogram of 500 maximal losses (), shown as a running cumulative in the right-hand plot. At each draw, the position of is marked by a red vertical dashed line.
n=1000
parent
d=500
M
n
M
n
In the limit of large , the Fisher–Tippett–Gnedenko theorem says that GEV(μ,σ,ξ), where the generalized extreme value function takes on one of the three types depending on the tail index of the parent distribution: type I Gumbel distribution (), type II Frechet distribution (), or type III reversed Weibull distribution (). A representative parent distribution is given for each type of tail-heaviness:
n
M
n
ξ
ξ=0
ξ>0
ξ<0
type I (light-tailed, ): is NormalDistribution[μ=0,σ=1]
ξ=0
parent
type II (heavy-tailed, ): is StudentTDistribution[μ=1,σ=2,ν=4]
ξ>0
parent
type III (lightest-tailed, ): is MinStableDistribution[μ=1,σ=1,γ=0.5]
ξ<0
parent
Because the size of the sample is finite (), the GEV-distributional fit gives only a rough estimate of the tail index . Thus, for type 1, the estimated tail index differs slightly from zero.
n=1000
ξ
The GEV distribution is a good depiction of the extreme tendency behavior—the extreme value theorem (EVT), just as the Gaussian distribution is a good depiction of the central tendency behavior—the central limit theorem (CLT).
Financial risk management is increasingly concerned with extreme losses, which are amenable to GEV characterization. Thus, EVT is increasingly a relevant tool in modern financial risk management, and a suitable companion to value-at-risk metric, especially for dealing with the risk of losses beyond the standard 95%, 99%, or 99.97% confidence levels.