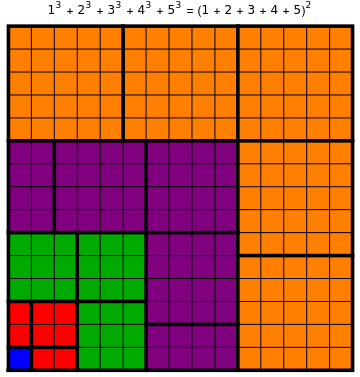
Fry's Geometric Demonstration of the Sum of Cubes

n

2

3

4

5

step

1

2

The sum of the first

n

cubes is given by the remarkable identity

3

1

+

3

2

+…+

3

n

=

2

(1+2+…+n)

=

2

n

(n+1)

4

.

Fry [1, 2] gave a geometrical proof of this result based on the slicing of

k×k×k

cubes into

k

k×k

square slabs and their assembly into a

n(n+1)

2

×

n(n+1)

2

square. For an even summand, one of the square slabs is cut in half for each end of the L-shape.