Fourier Coefficients of a Square Pulse
Fourier Coefficients of a Square Pulse
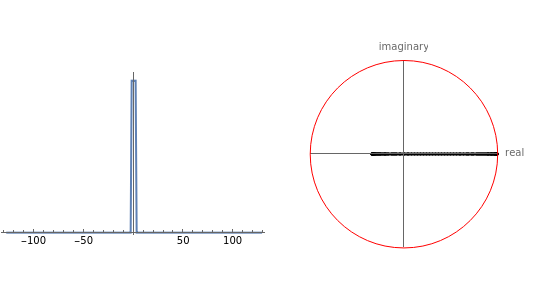
The real and imaginary parts of the Fourier components of a square wave (assumed periodic with a period of 256) as a function of the square wave width and position are shown in the graph on the right. The Fourier components are normalized to lie within or on the unit circle (shown in red). The vertical axis is the imaginary part and the horizontal axis is the real part, respectively. The graph on the left shows the square wave itself. The width is adjustable in unit steps from 1 to 256 and the position is adjustable in unit steps from -127 to +128. There are always 256 points in the graph on the right. Sometimes it may look like less but this is just because some points have the same value. Note that as the width is increased, more and more points move toward the origin in the graph on the right. This is because the wider the pulse, the more its Fourier spectrum is dominated by low frequencies, since the higher frequencies then have very small amplitude. One interesting case is to set the width to 2 and step the position by 1 unit at a time. The pattern evolves through many phases, some complex, some simple, some very regular and some that appear random.