Flow in a Vertical Channel with Walls at Different Temperatures

v

0

1.

U

2.

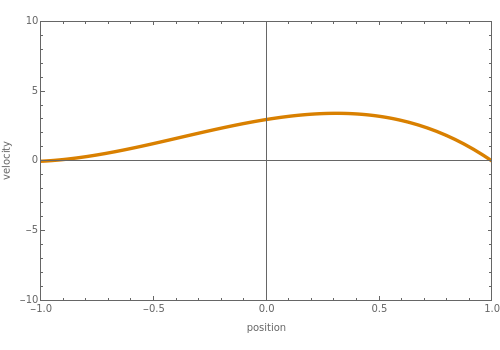
Consider a vertical parallel-plate channel of width

2H

with walls at different temperatures

T

1

and

T

2

,

T

2

>

T

1

. Two cases are studied: (1) pure free convection (i.e., the channel is closed at both ends and there is no net flow); and (2) mixed free and forced convection (a pressure gradient is present). The velocity (solution of the momentum equation) is given by

v

x

=

gβ(

T

2

-

T

m

)

2

H

6ν

η-

3

η

-

2

H

3



1

μ

d

dx

1-

2

η



,

where

g

is gravitational acceleration,

β

is the thermal expansion coefficient,

T

0

=

T

m

=

(

T

1

+

T

2

)

2

is the reference temperature taken equal to the mean temperature,

ν

is the kinematic viscosity,

μ

is the dynamic viscosity,

d

dx

is the pressure gradient, and

η=

y

H

is the dimensionless position.

The velocity can be expressed as

v

x

=

3

2



3

v

0

η-

3

η

+U1-

2

η



, where

U=-

2

H

3



1

μ

d

dx



is the mean velocity and

v

0

=

gβ(

T

2

-

T

1

)

2

H

18

3

ν

is the maximum velocity when the pressure gradient is zero.

If

U=0

and

T

2

≠

T

1

, one recovers pure free convection. When

T

2

=

T

1

, the velocity profile is the expected parabolic profile corresponding to a Poiseuille flow. In general, mixed free and forced convection is observed.