Expected Utility: Optimal Insurance

Wealth is 10 units. Possible loss is 9 with probability p.

amount insured q

4

price

0.54

probability p

0.3

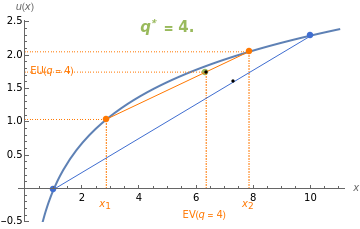
A lottery is played in which a person stands to obtain 1 or 10 units of wealth with probabilities

p

and

1-p

, respectively. A logarithmic utility function of wealth,

u(x)

, is plotted in dark blue. The blue chord represents the expected utility of the lottery,

E(u(x))=pu(1)+(1-p)u(10)

. Insurance that pays out

q

in the event of the unfavorable outcome of obtaining only 1 unit of wealth can be purchased. The cost of the insurance is the price of the insurance times the desired level of

q

. The orange chord represents the expected utility of the insured lottery. The optimal level of insurance yields the maximum expected utility possible, represented by the green dot.