Exothermic Continuous Stirred-Tank Reactor with Dynamically Varying Cooling Jacket
Exothermic Continuous Stirred-Tank Reactor with Dynamically Varying Cooling Jacket
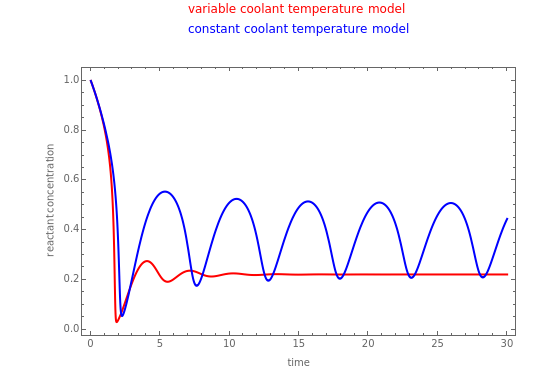
This Demonstration compares the kinetics of an exothermic reaction with a cooling jacket at constant temperature to a system in which the dynamics of the cooling jacket are taken into account.
The standard two-state CSTR (continuous stirred-tank reactor) model describing an exothermic diabatic first-order irreversible reaction can be represented by a pair of ordinary dimensionless differential equations [1]
AB
d
C
A
dt
D
a
C
A
T/(1+T/γ)
e
C
A
0
C
A
and
dT
dt
D
a
C
A
T/(1+T/γ)
e
T
c
C
0
where and are the concentration of reactant and reactor temperature, respectively, is the constant coolant temperature, is the Damköhler number, is the activation energy, is the reactor flow rate, is the heat transfer coefficient, and is time.
C
A
T
A
T
c
D
a
γ
Q
δ
t
When the dynamics of the cooling jacket are considered, is a variable and an additional energy balance around the cooling jacket yields a third dimensionless differential equation
T
c
d
T
c
dt
δ
1
T
c
0
T
c
δ
2
T
c
where and are the reactor-to-cooling-jacket volume ratio and density heat capacity ratio, respectively, and is the cooling jacket flow rate.
δ
1
δ
2
q
Plots of the functions and are shown for the standard two-equation system and for the three-equation system that incorporates the dynamics of the cooling jacket for user-selected values of time , Damköhler number , coolant flow rate , and initial coolant temperature . The parameters are taken as with initial conditions . The addition of the third equation shows that much more complex behavior than a simple time lag can occur and this can significantly affect the behavior and stability of a reactor.
C
A
T
t
D
a
q
T
c
0
(Q,β,δ,,,γ)=(1,11,1.5,10,0.11,20)
δ
1
δ
2
,=(1,0)
C
A
0
T
0