Erdös-Szekeres Tableaux
Erdös-Szekeres Tableaux
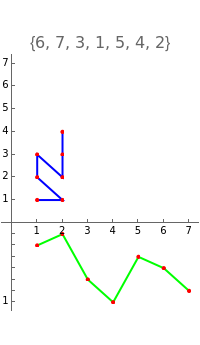
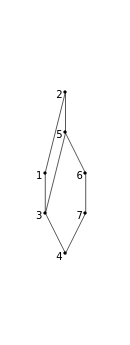
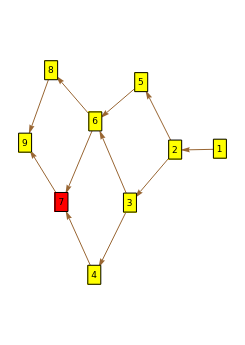
The Erdös–Szekeres tableau of a permutation is the sequence of points where (respectively ) is the length of the longest increasing (respectively decreasing) subsequence ending at . Since different permutations can have the same Erdös–Szekeres tableau (EST) (e.g. and both have the same "N-shaped" EST), there is an equivalence relation on permutations . The poset is defined by taking the intersection over all orderings induced by elements of . Informally, the poset records those relations that can be recovered from the EST. The lattice is defined on , where is in the covering relation if and differ by an adjacent transposition (which can be viewed as an edge label) and precedes lexicographically.
(σ)
σ=(,…,)
a
1
a
n
n
{(,)}
x
i
y
i
i=1
x
i
y
i
a
i
(2,1,4,3)
(3,1,4,2)
[σ]={σ~τ|(σ)=(τ)}
[σ]
[σ]
(τ,τ')
τ
τ'
τ
τ'