Elliptic Epitrochoid

base ellipse

eccentricity

0.866

rolling ellipse

circumference ratio

0.5

1.

1.5

2.

2.5

eccentricity

0.866

starting angular position

0

generator position

move to center

roll the ellipse

0.

zoom

1.2

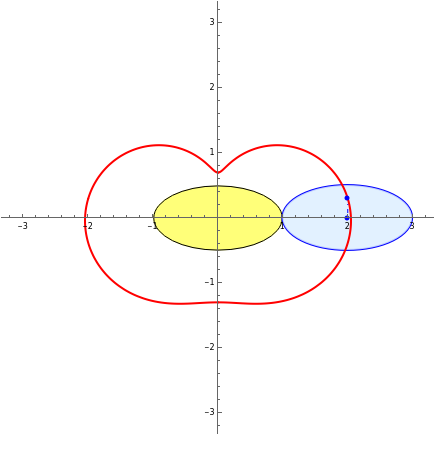
This Demonstration traces the path of a point (known as the pole or generator) fixed to an ellipse that rolls without slipping around a stationary base ellipse.

If the circumference ratio between the ellipses is the rational number

p

q

, a closed curve is obtained after

q

complete revolutions of the rolling ellipse around the base. By then the rolling ellipse will have made

p+q

revolutions around its center.

In this Demonstration, the circumference ratios are either integers (

q=1

) or of the form

p

2

(

q=2

). Consequently, a curve closes after one or two revolutions of the rolling ellipse around the base ellipse.

Moving the pole inside or outside the rolling ellipse makes the elliptic epitrochoid either curtate or prolate.

Changing the eccentricity of either ellipse creates a great variety of curves.