Electric Field of a Line of Charge

discrete charge elements

20

length of line charge l/m

1

line charge q/

C

9

9

10

1

θ

1

= 14.0362° |

θ

2

= 50.1944° | electric field = 2.24401 N/C | θ = 33.3866°

According to the principle of superposition, the field generated by a collection of charges is the sum of the electric fields generated by each of the individual charges.

E

=

1

4

πϵ

0

n

∑

i=1

E

i

=

1

4

πϵ

0

n

∑

i=1

q

i

2

r

i



r

i

,

E

i

1

4

πϵ

0

q

i

2

r

i



r

i

,



r

i

=



r

i

r

.

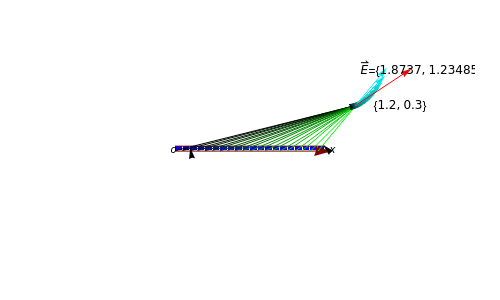
If the charge distribution is continuous, then the total electric field can be calculated by integrating the electric fields

d

E

generated by each small element of charge

dq

in the distribution.

E

=∫d

E

=

1

4

πϵ

0





r

2

r

dq

,

d

E



r

2

r

dq

,



r

=



r

,

dq=λdl

for a linear distribution, where

λ

stands for the linear charge density.

This Demonstration illustrates the electric field generated by a line of charge.