Eigenvalues for a Pure Quartic Oscillator

matrix dimension

1

2

3

4

5

6

7

8

parameter ω

2

calculated eigenvalues	0.546875	1.73438
WKB eigenvalues	0.344127	1.48895	2.94224	4.60804	6.44231	8.41864	10.519	12.7303

The oscillator with a quartic anharmonicity, with Hamiltonian

H=

2

p

2μ

+

1

2

k

2

x

+

1

4

λ

4

x

has been extensively treated in the literature. Consider the pure quartic oscillator, in which the quadratic term is missing:

k=0

. For simplicity, take

μ=λ=1

. The Schrödinger equation thus reduces to

-

1

2

ψ''(x)+

1

4

x

ψ(x)=Eψ(x)

.

No analytic solution has been found, but accurate numerical computations have been carried out [1]. This Demonstration applies the operator method [2], a generalization of the canonical operator formulation for the harmonic oscillator, for potential energies that are functions of even powers of

x

. For larger values of the matrix dimension, the results obtained here are comparable with the published results.

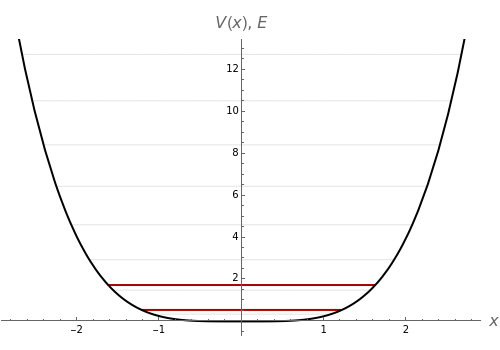
The computation results in a secular equation for the eigenvalues, which are plotted as red lines on the graph superposed on the potential energy curve. The number of eigenvalues shown is equal to the selected matrix dimension. For comparison, the first eight eigenvalues according to the WKB method are shown as thin gray lines.