Eigenvalues and the Principal Invariants of a Linear Map

I

3

0.225

The quantities

I

1

=tr(A)

,

I

2

=

1

2



2

tr(A)

-tr(

2

A

)

,

I

3

=det(A)

are called the principal invariants of the matrix

A

.

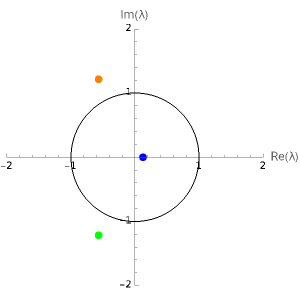
Drag the point in the

I

1

-

I

2

plane and move the slider

I

3

to display the corresponding eigenvalues around the unit circle in the complex plane.

In the left-hand graphic, the discriminant is negative in the purple region; in the orange region, the eigenvalues have modulus less than one.

The eigenvalues of the matrix

A

determine how the flow of a differential map or the orbit of a discrete map behaves.